
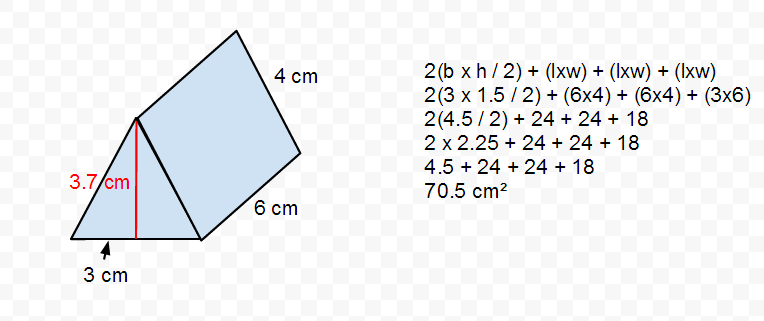
( Note: The h refers to the altitude of the prism, not the height of the trapezoid. ( Note: The h refers to the altitude of the prism, not the height of the trapezoid.) Find (a) LA (b) TA and (c) V.įigure 6 An isosceles trapezoidal right prism. Theorem 89: The volume, V, of a right prism with a base area B and an altitude h is given by the following equation.Įxample 3: Figure 6 is an isosceles trapezoidal right prism. Thus, the volume of this prism is 60 cubic inches. Because the prism has 5 such layers, it takes 60 of these cubes to fill this solid. This prism can be filled with cubes 1 inch on each side, which is called a cubic inch. In Figure 5, the right rectangular prism measures 3 inches by 4 inches by 5 inches.įigure 5 Volume of a right rectangular prism. The volume of a solid is the number of cubes with unit edge necessary to entirely fill the interior of the solid. The interior space of a solid can also be measured.Ī cube is a square right prism whose lateral edges are the same length as a side of the base see Figure 4. Lateral area and total area are measurements of the surface of a solid. The altitude of the prism is given as 2 ft. Example: What is the volume of a prism where the base area is 25 m 2 and which is 12 m long: Volume Area × Length. The perimeter of the base is (3 + 4 + 5) ft, or 12 ft.īecause the triangle is a right triangle, its legs can be used as base and height of the triangle. The base of this prism is a right triangle with legs of 3 ft and 4 ft (Figure 3).įigure 3 The base of the triangular prism from Figure 2. Theorem 88: The total area, TA, of a right prism with lateral area LA and a base area B is given by the following equation.Įxample 2: Find the total area of the triangular prism, shown in Figure 2. Because the bases are congruent, their areas are equal.

The total area of a right prism is the sum of the lateral area and the areas of the two bases. Theorem 87: The lateral area, LA, of a right prism of altitude h and perimeter p is given by the following equation.Įxample 1: Find the lateral area of the right hexagonal prism, shown in Figure 1. The lateral area of a right prism is the sum of the areas of all the lateral faces. These are known as a group as right prisms. In certain prisms, the lateral faces are each perpendicular to the plane of the base (or bases if there is more than one).
We can construct rectangular prisms by stacking up cubes.

It has dimensions: length, width and height. Formulas: Perimeter, Circumference, Area Volume of a Right Rectangular Prism Rectangular Prisms Rectangular prisms are three-dimensional figures made up of six faces of rectangles.Proving that Figures Are Parallelograms.Triangle Inequalities: Sides and Angles.Special Features of Isosceles Triangles.Classifying Triangles by Sides or Angles.Lines: Intersecting, Perpendicular, Parallel.


 0 kommentar(er)
0 kommentar(er)
